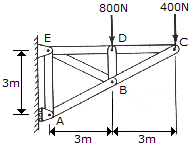
Determine the force in each member of the truss and indicate whether the members are in tension or compression.

Determine the force in each member of the truss and indicate whether the members are in tension or compression.

Solution

First consider a free body diagram for the whole truss structure to find the reactions at supports E and A by applying the equations of equilibrium for its external forces.

So taking summation of moment about E = 0, 3Ra-3(800)-6(400) = 0.

Ra = 1600 N.

Sum of horizontal forces = Re(x)-800-400 = 0; Re(x) = 1200 N.

Sum of vertical forces = Re(y)-Ra = 0; Re(y) = 1600 N.

Considering each member force to be a tension, each joint will be analyzed so taking joint C,

Sum of horizontal forces = 400+F(CB) sin(26.57) = 0, F(CB) = -894 N T or F(CB) = 894 N C.

Sum of vertical forces = -F(CB) cos (26.57)-F(CD) = 0; F(CD) = 800 N T.

At joint D, F(DC) = F(DE) = 800 N T F(DB) = -800 N T = 800 N C.

At joint E, Sum of vertical forces = F ED)+F(EB) sin(63.43)-Re(y) = 0.

F(EB) = (Re(Y)-F(ED))/sin(63.43) = 894 N T.

Sum of horizontal forces = F(EA) = F(EB) cos(63.43) = Re(x).

F(EA) = 1200-894 cos(63.43) = 800 N T.

At joint B, Sum of horizontal forces = 0.

F(BA) cos(63.43)-F(BC) cos(63.43)-F(BE) cos(63.43)-F(BD) = 0.

F (BA) = -1789 N T = 1789 N C.