Determine the internal normal force, shear force and bending moment acting at point C in the beam shown in the figure.

 Determine the internal normal force, shear force and bending moment acting at point C in the beam shown in the figure.

Reference: Structural Analysis by R C Hibbeler.

Solutio

L = 4 m,n:

VB = 0.5*5*2 = 5 kN

please note that at supports, MA = 0.0 kNm, and MB = -0.5*5*2*2/3 = -3.334 kN m

Using the static equilibrium conditions, algebraic sum of moments at the left end is equated to zero.
Hence, RB = [(MB – MA – VB*(L -2) -5.0 * (2.0) * 1.0 ] / (L-2.0)
Hence, RB = 11.667 kN
Also, RA + RB = 5*2 + VB = 15 kN.
Solving gives, RA = 3.334 kN,

End support reactions are: Vertical Reactions, RA = 3.334 kN, and RB = 11.664 kN

In between A and B,
for 0.0m <= x <= 2.0m:
Shear, Vx = 3.334 – 5.0*x

Moment, Mx = VA(x-0.0) + -5.0(x -0.0)^2/2 = -2.5x^2 + 3.334*x

In between B and the right end,

for 2.0m <= x <= 4.0m:
Shear, Vx = 1.25x2 – 10.0x + 20.0

Moment, Mx = 0.41667x^3 – 5.0*x^2 + 20.0*x – 26.667

Shear Force and Bending Moment Diagram, F4-4, Structural Analysis by R C Hibbeler.

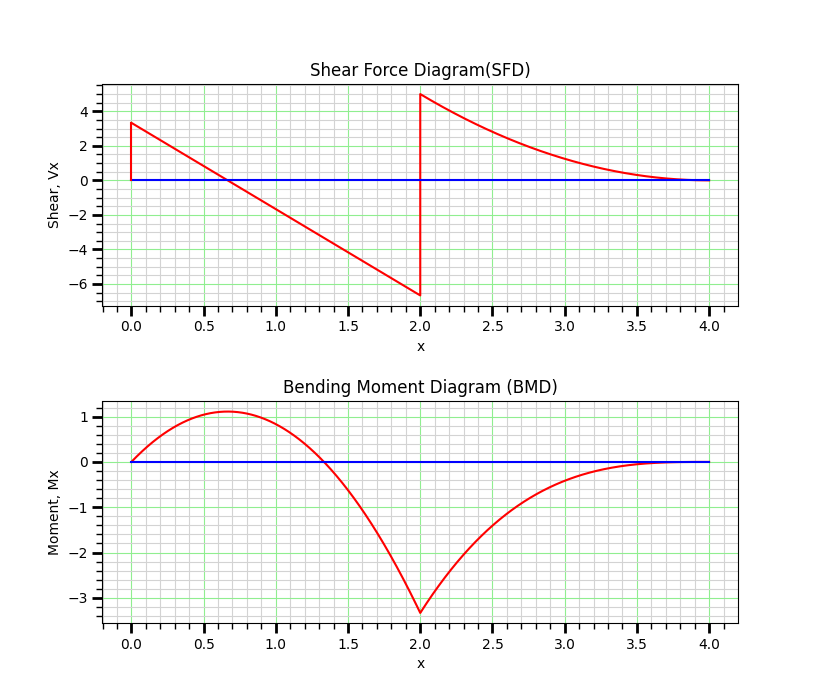
Maximum +ve Bending Moment, Mmax = 1.111 kN-m
at x = 0.667 m from the left end.

Maximum -ve Bending Moment, Mmin = -3.333 kN-m
at x = 2.0 m from the left end.

At C, x = 1 m,

Axial Force, NC = 0,

Shear Force, VC = 3.334 – 5.0*1 = -1.6667 kN

Bending Moment, MC = -2.5* 12 + 3.334*1 = 0.8334 kN-m