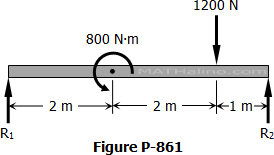
For the beam shown in Fig., determine the value of EIδ at 2 m and 4 m from the left support.

For the beam shown in Fig., determine the value of EIδ at 2 m and 4 m from the left support.

 

 

Solution 

ΣMR2=0ΣMR2=0

5R1=800+1200(1)$5R_1=800+1200(1)$

R1=400 N$R_1=400\text{N}$
 

ΣMR1=0$\mathrm{\Sigma }{M}_{R1}=0$

5R2+800=1200(4)$5R_2+800=1200(4)$

R2=800 N$R_2=800\text{N}$
 

M1=M4=0$M_1=M_4=0$

M2=2R1−800=2(400)−800=0$M_2=2R_1-800=2(400)-800=0$

M3=1R2=800 N⋅m$M_3=1R_2=800\text{N}\cdot \text{m}$
 

 

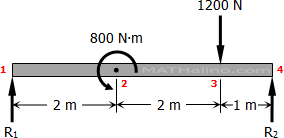
For the deflection at point 2 (consider the span 1-2-4)

L1=2 m$L_1=2\text{m}$   ←   span 1 to 2

L2=3 m$L_2=3\text{m}$   ←   span 2 to 4
 

M1L1+2M2(L1+L2)+M4L2+6A1a¯1L1+6A2b¯2L2=6EI(h1L1+h4L2)$M_1{L}_1+2M_2(L_1+L_2)+M_4{L}_2+{\displaystyle \frac{6A_1{\overline{a}}_1}{L_1}}+{\displaystyle \frac{6A_2{\overline{b}}_2}{L_2}}=6EI\left({\displaystyle \frac{h_1}{L_1}}+{\displaystyle \frac{h_4}{L_2}}\right)$

0+0+0−−8002[3(22)−22]+1200(1)3(32−12)=6EI(h2+h3)$0+0+0-{\displaystyle \frac{-800}{2}}[3(2^2)-2^2]+{\displaystyle \frac{1200(1)}{3}}(3^2-1^2)=6EI\left({\displaystyle \frac{h}{2}}+{\displaystyle \frac{h}{3}}\right)$

3200+3200=6EI(5h6)$3200+3200=6EI\left({\displaystyle \frac{5h}{6}}\right)$

6400=5EIh$6400=5EIh$

h=1280EI$h={\displaystyle \frac{1280}{EI}}$
 

The positive sign indicates that points 1 and 4 are above point 2
δ2=1280EI  downward${\delta }_2={\displaystyle \frac{1280}{EI}}\text{ downward}$           answer

 

For the deflection at point 3 (consider the span 1-3-4)

L1=4 m$L_1=4\text{m}$   ←   span 1 to 3

L2=1 m$L_2=1\text{m}$   ←   span 3 to 4
 

M1L1+2M3(L1+L2)+M4L2+6A1a¯1L1+6A2b¯2L2=6EI(h1L1+h4L2)$M_1{L}_1+2M_3(L_1+L_2)+M_4{L}_2+{\displaystyle \frac{6A_1{\overline{a}}_1}{L_1}}+{\displaystyle \frac{6A_2{\overline{b}}_2}{L_2}}=6EI\left({\displaystyle \frac{h_1}{L_1}}+{\displaystyle \frac{h_4}{L_2}}\right)$

0+2(800)(4+1)+0−−8004[3(22)−42]+0=6EI(h4+h1)$0+2(800)(4+1)+0-{\displaystyle \frac{-800}{4}}[3(2^2)-4^2]+0=6EI\left({\displaystyle \frac{h}{4}}+{\displaystyle \frac{h}{1}}\right)$

8000−800=6EI(5h4)$8000-800=6EI\left({\displaystyle \frac{5h}{4}}\right)$

7200=152EIh$7200=\frac{15}{2}EIh$

h=960EI$h={\displaystyle \frac{960}{EI}}$
 

The positive sign indicates that points 1 and 4 are above point 3
δ3=960EI  downward${\delta }_3={\displaystyle \frac{960}{EI}}\text{ downward}$           answer