For three events AA, BB, and CC, we know that AA and CC are independent, BB and CC are independent, AA and BB are disjoint, P(A∪C)=23,P(B∪C)=34,P(A∪B∪C)=1112P(A∪C)=23,P(B∪C)=34,P(A∪B∪C)=1112 Find P(A),P(B)P(A),P(B), and P(C)P(C).

 problem

For three events 

A$A$, B$B$, and C$C$, we know that

• A$A$ and C$C$ are independent,
• B$B$ and C$C$ are independent,
• A$A$ and B$B$ are disjoint,
• P(A∪C)=23,P(B∪C)=34,P(A∪B∪C)=1112$P(A\cup C)=\frac{2}{3},P(B\cup C)=\frac{3}{4},P(A\cup B\cup C)=\frac{11}{12}$

Find P(A),P(B)$P(A),P(B)$, and P(C)$P(C)$.

• Solution

  • We can use the Venn diagram in Figure 1.26 to better visualize the events in this problem. We assume P(A)=a,P(B)=b$P(A)=a,P(B)=b$, and P(C)=c$P(C)=c$. Note that the assumptions about independence and disjointness of sets are already included in the figure.

    

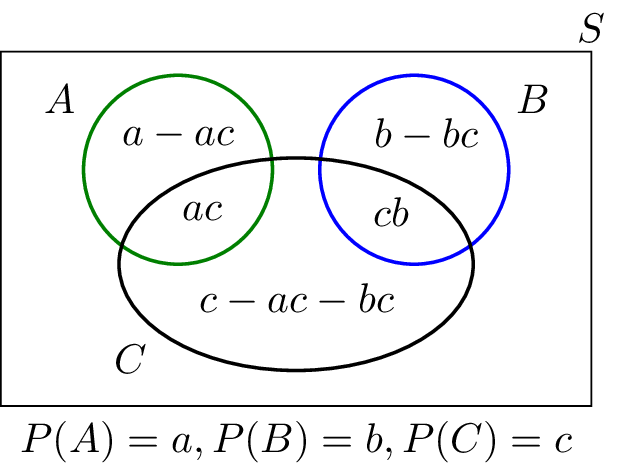
    - Venn diagram for Problem 3.

    Now we can write

    P(A∪C)=a+c−ac=23;$$P(A\cup C)=a+c-ac=\frac{2}{3};$$
    P(B∪C)=b+c−bc=34;$$P(B\cup C)=b+c-bc=\frac{3}{4};$$
    P(A∪B∪C)=a+b+c−ac−bc=1112.$$P(A\cup B\cup C)=a+b+c-ac-bc=\frac{11}{12}.$$
    By subtracting the third equation from the sum of the first and second equations, we immediately obtain c=12$c=\frac{1}{2}$, which then gives a=13$a=\frac{1}{3}$ and b=12$b=\frac{1}{2}$.