In my town, it's rainy one third of the days. Given that it is rainy, there will be heavy traffic with probability 1212, and given that it is not rainy, there will be heavy traffic with probability 1414. If it's rainy and there is heavy traffic, I arrive late for work with probability 1212. On the other hand, the probability of being late is reduced to 1818 if it is not rainy and there is no heavy traffic. In other situations (rainy and no traffic, not rainy and traffic) the probability of being late is 0.250.25. You pick a random day. What is the probability that it's not raining and there is heavy traffic and I am not late? What is the probability that I am late? Given that I arrived late at work, what is the probability that it rained that day?

 Problem

In my town, it's rainy one third of the days. Given that it is rainy, there will be heavy traffic with probability 

12$\frac{1}{2}$, and given that it is not rainy, there will be heavy traffic with probability 14$\frac{1}{4}$. If it's rainy and there is heavy traffic, I arrive late for work with probability 12$\frac{1}{2}$. On the other hand, the probability of being late is reduced to 18$\frac{1}{8}$ if it is not rainy and there is no heavy traffic. In other situations (rainy and no traffic, not rainy and traffic) the probability of being late is 0.25$0.25$. You pick a random day.

1. What is the probability that it's not raining and there is heavy traffic and I am not late?
2. What is the probability that I am late?
3. Given that I arrived late at work, what is the probability that it rained that day?

• Solution

  • Let R$R$ be the event that it's rainy, T$T$ be the event that there is heavy traffic, and L$L$ be the event that I am late for work. As it is seen from the problem statement, we are given conditional probabilities in a chain format. Thus, it is useful to draw a tree diagram. Figure 1.27 shows a tree diagram for this problem. In this figure, each leaf in the tree corresponds to a single outcome in the sample space. We can calculate the probabilities of each outcome in the sample space by multiplying the probabilities on the edges of the tree that lead to the corresponding outcome.

    

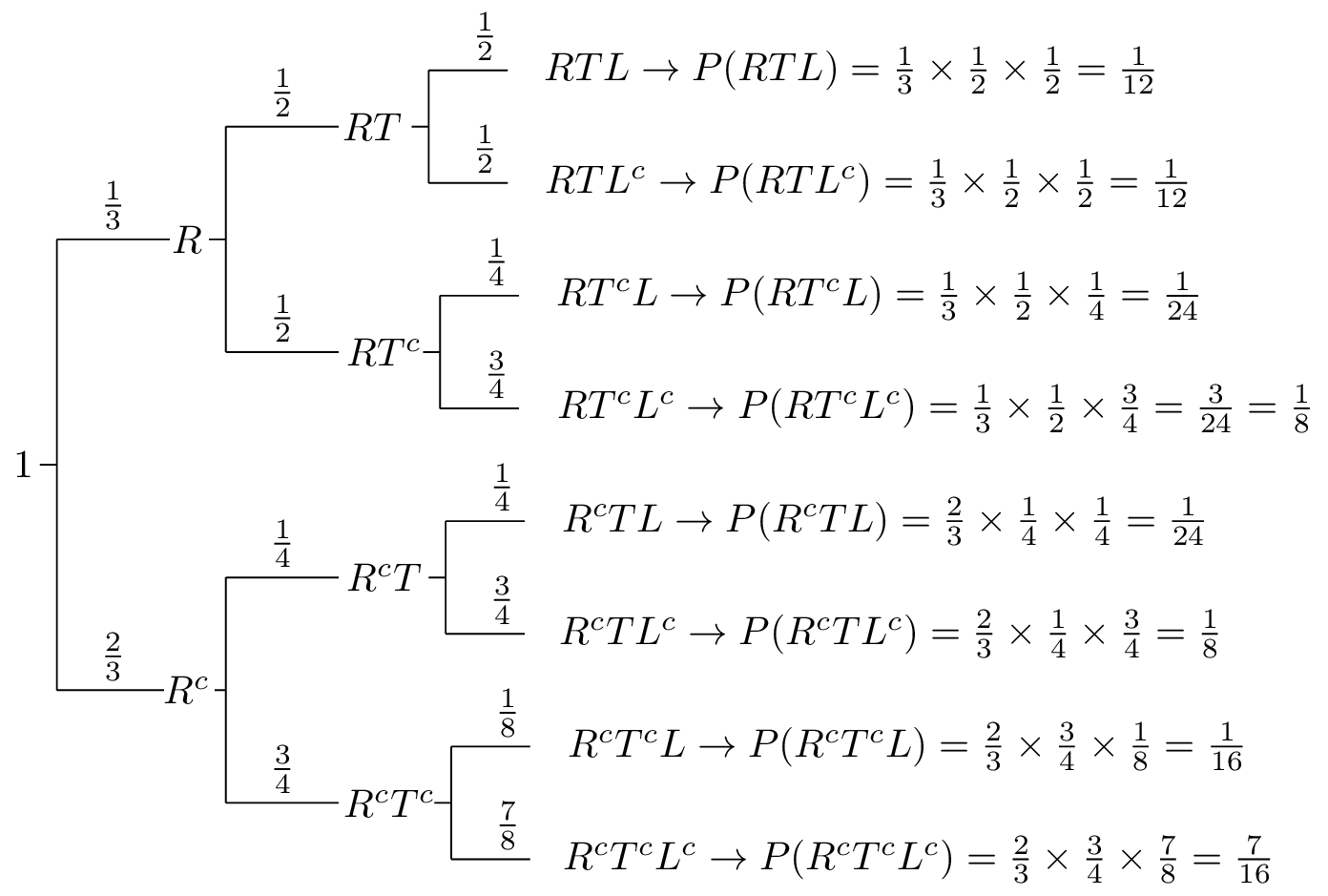
    Fig.1.27 - Tree diagram for Problem 5.

    1. The probability that it's not raining and there is heavy traffic and I am not late can be found using the tree diagram which is in fact applying the chain rule:
       
       

       P(Rc∩T∩Lc)$P(R^c\cap T\cap L^c)$	=P(Rc)P(T|Rc)P(Lc|Rc∩T)$=P(R^c)P(T|R^c)P(L^c|R^c\cap T)$
       	=23⋅14⋅34$=\frac{2}{3}\cdot \frac{1}{4}\cdot \frac{3}{4}$
       	=18$=\frac{1}{8}$.

       
       
    2. The probability that I am late can be found from the tree. All we need to do is sum the probabilities of the outcomes that correspond to me being late. In fact, we are using the law of total probability here.
       
       

       P(L)$P(L)$	=P(R,T,L)+P(R,Tc,L)+P(Rc,T,L)+P(Rc,Tc,L)$=P(R,T,L)+P(R,T^c,L)+P(R^c,T,L)+P(R^c,T^c,L)$
       	=112+124+124+116$=\frac{1}{12}+\frac{1}{24}+\frac{1}{24}+\frac{1}{16}$
       	=1148$=\frac{11}{48}$.

       
       
    3. We can find P(R|L)$P(R|L)$ using P(R|L)=P(R∩L)P(L)$P(R|L)=\frac{P(R\cap L)}{P(L)}$. We have already found P(L)=1148$P(L)=\frac{11}{48}$, and we can find P(R∩L)$P(R\cap L)$ similarly by adding the probabilities of the outcomes that belong to R∩L$R\cap L$. In particular,
       
       

       P(R∩L)$P(R\cap L)$	=P(R,T,L)+P(R,Tc,L)$=P(R,T,L)+P(R,T^c,L)$
       	=112+124$=\frac{1}{12}+\frac{1}{24}$
       	=18$=\frac{1}{8}$.

       
       Thus, we obtain
       
       

       P(R|L)$P(R|L)$	=P(R∩L)P(L)$=\frac{P(R\cap L)}{P(L)}$
       	=18.4811$=\frac{1}{8}.\frac{48}{11}$
       	=611$=\frac{6}{11}$.