The five-story office steel building shown in Figure 2.7 is laterally braced with steel special moment resisting frames, and it measures 75 ft by 100 ft in the plan. The building is located in New York City. Using the ASCE 7-16 equivalent lateral force procedure, determine the lateral force that will be applied to the fourth floor of the structure. The roof dead load is 32 psf, the floor dead load (including the partition load) is 80 psf, and the flat roof snow load is 40 psf. Ignore the weight of cladding. The design spectral acceleration parameters are SDS = 0.28, and SD1 = 0.11.

 The five-story office steel building shown in Figure 2.7 is laterally braced with steel special moment resisting frames, and it measures 75 ft by 100 ft in the plan. The building is located in New York City. Using the ASCE 7-16 equivalent lateral force procedure, determine the lateral force that will be applied to the fourth floor of the structure. The roof dead load is 32 psf, the floor dead load (including the partition load) is 80 psf, and the flat roof snow load is 40 psf. Ignore the weight of cladding. The design spectral acceleration parameters are SDS = 0.28, and SD1 = 0.11.

Fig. 2.7. Five – story office building.

Solution

SDS = 0.28 and SD1 = 0.11 (given).

R = 8 for special moment resisting steel frame (see Table 2.13).

An office building is in occupancy risk category II, so Ie = 1.0 (see Table 2.9).

Calculate the approximate fundamental natural period of the building Ta.

Ct = 0.028 and x = 0.8 (from Table 2.12 for steel moment resisting frames).

ℎn = Roof height = 52.5 ft

Determine the dead load at each level. Since the flat roof snow load given for the office building is greater than 30 psf, 20% of the snow load must be included in the seismic dead load computations.

The weight assigned to the roof level is as follows:

Wroof = (32 psf)(75 ft)(100 ft) + (20%)(40psf)(75 ft)(100 ft) = 300,000 lb

The weight assigned to all other levels is as follows:

Wi = (80 psf)(75ft)(100 ft) = 600,000 lb

The total dead load is as follows:

WTotal = 300,000 lb + (4)(600,000 lb) = 2700 k

Calculate the seismic response coefficient Cs.

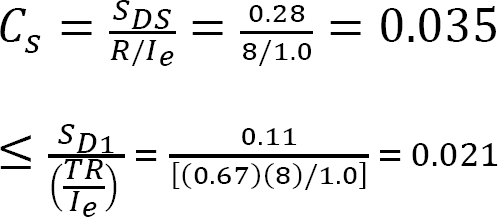
Therefore, Cs = 0.021 > 0.01

Determine the seismic base shear V.

V = CsW = (0.021)(2700 kips) = 56.7k

Calculate the lateral force applied to the fourth floor.

2.1.4.5 Hydrostatic and Earth Pressures