A PI is located at 55+69.23 with a deflection angle between tangents of 85°00'00"R. The compound curve must begin 463.64 ft before the PI and end 405.60 ft after. Central angles of the two curves are 30°00'00" and 55°00'00", respectively. Determine the radius of each curve,

 A PI is located at 55+69.23 with a deflection angle between tangents of 85°00'00"R. The compound curve must begin 463.64 ft before the PI and end 405.60 ft after. Central angles of the two curves are 30°00'00" and 55°00'00", respectively.

Determine the radius of each curve,

Sketch:

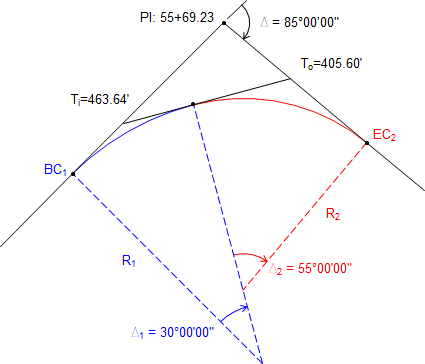
Because we only have angles of the vertex triangle with no distances (and insufficient given data to compute any), the curve system can't be solved that way. Instead, we will use the traverse method.

To start, the curve system is rotated to make the initial radial line run North. Then using right angles and Δs, bearings (or azimuths) of the other lines can be determined.

Updated sketch with bearings:

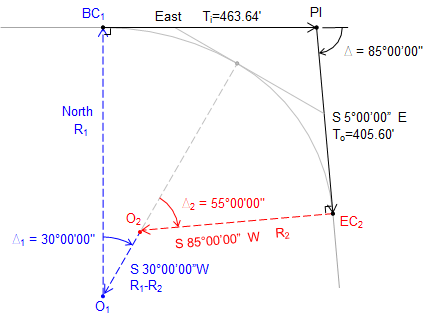
Compute Latitudes and Departures:

Line	Bearing	Length	Latitude	Departure
O1-BC1	North	R1	R1	0.00
BC1-PI	East	463.64	0.00	463.64
PI-EC2	S 5°00'00"E	405.60	-405.60 x cos(5°00'00")	+405.60 x sin(5°00'00")
EC2-O2	S 85°00'00"W	R2	-R2 x cos(85°00'00")	-R2 x sin(85°00'00")
O2-O1	S 30°00'00"W	R1-R2	-(R1-R2) x cos(30°00'00")	-(R1-R2) x sin(30°00'00")

 

 Sum and reduce the Latitudes:

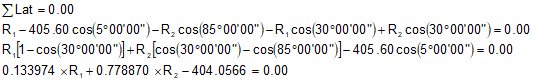
Sum and reduce the Departures:

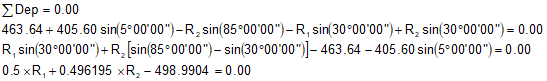
We have two equations with unknowns R1 and R2. Solve them simultaneously. We'll use substitution.

Solve the Latitude summation for R1

Substitute the equation for R1 in the Departures summation and solve R2:

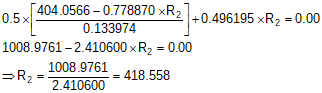
Solve R1:

With R1 and R2 computed, we have two geometric attributes for each curve. Using Chapter C. Horizontal Curves equations, their remaining attributes can be determined.