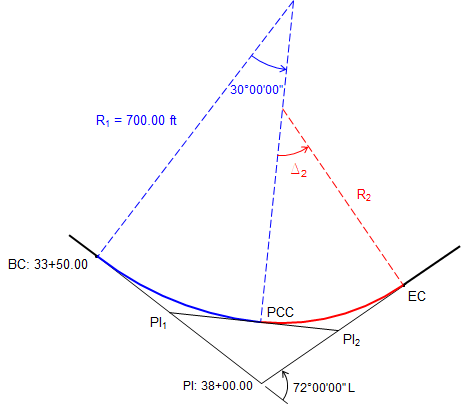
A PI is located at station 38+00.00 with a left deflection of 72°00'00"L. The compound curve begins at sta 33+50.00. The first curve has a 700.00 ft radius and 30°00'00" central angle.
Determine the radius and central angle of the second curve and the length of both curves.
Sketch:
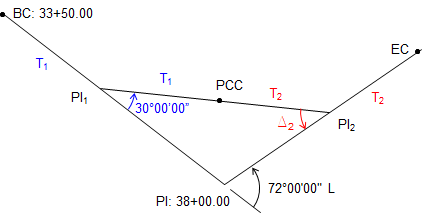
We'll try a vertex triangle solution. Isolate the triangle and label the tangents:
Since we have the radius and central angle of the first curve, we can compute its tangent:
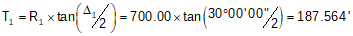
Compute Δ2 using Equation D-1
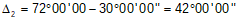
Determine the distance from the PI1 to the PI which is a side of the triangle.
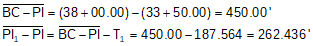
The distance between PI1 and PI2 is the sum of the curve tangents. Using the Law of Sines and the known T1, we can compute T2.
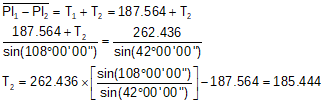
Using T2 and Δ2, R2 can be determined.
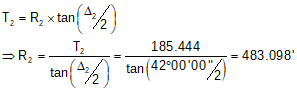
Finally, compute each curve's length.
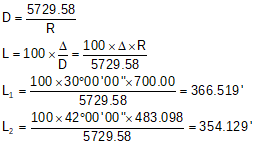
No comments:
Post a Comment