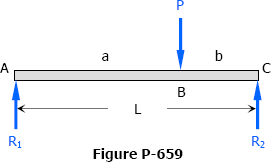
A simple beam supports a concentrated load placed anywhere on the span, as shown in Fig. P-659. Measuring x from A, show that the maximum deflection occurs at x = √[(L2 - b2)/3].

A simple beam supports a concentrated load placed anywhere on the span, as shown in Fig. P-659. Measuring x from A, show that the maximum deflection occurs at x = √[(L2 - b2)/3].
 

Solution                              

 ΣMR2=0ΣMR2=0

LR1=Pb$L{R}_1=Pb$

R1=Pb/L$R_1=Pb/L$
 

ΣMR1=0$\mathrm{\Sigma }{M}_{R1}=0$

LR2=Pa$L{R}_2=Pa$

R2=Pa/L$R_2=Pa/L$
 

yx=PbL${\displaystyle \frac{y}{x}}={\displaystyle \frac{Pb}{L}}$

y=PbLx$y={\displaystyle \frac{Pb}{L}}x$
 

tA/D=1EI(AreaAD)X¯A$t_{A/D}={\displaystyle \frac{1}{EI}}(Are{a}_{AD}){\overline{X}}_A$

tA/D=1EI[12xy(23x]$t_{A/D}={\displaystyle \frac{1}{EI}}[\frac{1}{2}xy(\frac{2}{3}x]$

tA/D=1EI[13x2y]$t_{A/D}={\displaystyle \frac{1}{EI}}[\frac{1}{3}{x}^{2}y]$

tA/D=1EI[13x2(PbLx)]$t_{A/D}={\displaystyle \frac{1}{EI}}\left[\frac{1}{3}{x}^2\left({\displaystyle \frac{Pb}{L}}x\right)\right]$

tA/D=1EIPb3Lx3$t_{A/D}={\displaystyle \frac{1}{EI}}{\displaystyle \frac{Pb}{3L}}{x}^3$
 

tC/D=1EI(AreaCD)X¯C$t_{C/D}={\displaystyle \frac{1}{EI}}(Are{a}_{CD}){\overline{X}}_C$

tC/D=1EI[16(L−x)2(Pb−y)+12(L−x)2y−16Pb3]$t_{C/D}={\displaystyle \frac{1}{EI}}[\frac{1}{6}(L-x{)}^2(Pb-y)+\frac{1}{2}(L-x{)}^{2}y-\frac{1}{6}P{b}^3]$

tC/D=1EI[16(L−x)2(Pb−PbLx)+12(L−x)2(PbLx)−16Pb3]$t_{C/D}={\displaystyle \frac{1}{EI}}\left[\frac{1}{6}(L-x{)}^2\left(Pb-{\displaystyle \frac{Pb}{L}}x\right)+\frac{1}{2}(L-x{)}^2\left({\displaystyle \frac{Pb}{L}}x\right)-\frac{1}{6}P{b}^3\right]$

tC/D=1EI[16Pb(L−x)2(1−xL)+12Pb(L−x)2(xL)−16Pb3]$t_{C/D}={\displaystyle \frac{1}{EI}}\left[\frac{1}{6}Pb(L-x{)}^2\left(1-{\displaystyle \frac{x}{L}}\right)+\frac{1}{2}Pb(L-x{)}^2\left({\displaystyle \frac{x}{L}}\right)-\frac{1}{6}P{b}^3\right]$

tC/D=1EI[Pb6L(L−x)3+Pb2L(L−x)2x−Pb36]$t_{C/D}={\displaystyle \frac{1}{EI}}\left[{\displaystyle \frac{Pb}{6L}}(L-x{)}^3+{\displaystyle \frac{Pb}{2L}}(L-x{)}^{2}x-{\displaystyle \frac{P{b}^3}{6}}\right]$
 

From the figure:
tA/D=tC/D$t_{A/D}=t_{C/D}$

1EIPb3Lx3=1EI[Pb6L(L−x)3+Pb2L(L−x)2x−Pb36]${\displaystyle \frac{1}{EI}}{\displaystyle \frac{Pb}{3L}}{x}^3={\displaystyle \frac{1}{EI}}\left[{\displaystyle \frac{Pb}{6L}}(L-x{)}^3+{\displaystyle \frac{Pb}{2L}}(L-x{)}^{2}x-{\displaystyle \frac{P{b}^3}{6}}\right]$

Pb3Lx3=Pb6L(L−x)3+Pb2L(L−x)2x−Pb36${\displaystyle \frac{Pb}{3L}}{x}^3={\displaystyle \frac{Pb}{6L}}(L-x{)}^3+{\displaystyle \frac{Pb}{2L}}(L-x{)}^{2}x-{\displaystyle \frac{P{b}^3}{6}}$

2x3L=(L−x)3L+3(L−x)2xL−b2${\displaystyle \frac{2x^3}{L}}={\displaystyle \frac{(L-x{)}^3}{L}}+{\displaystyle \frac{3(L-x{)}^{2}x}{L}}-b^2$

2x3=(L−x)3+3(L−x)2x−Lb2$2x^3=(L-x{)}^3+3(L-x{)}^{2}x-L{b}^2$

2x3=(L3−3L2x+3Lx2−x3)+3(L2−2Lx+x2)x−Lb2$2x^3=(L^3-3L^{2}x+3L{x}^2-x^3)+3(L^2-2Lx+x^2)x-L{b}^2$

2x3=L3−3L2x+3Lx2−x3+3L2x−6Lx2+3x3−Lb2$2x^3=L^3-3L^{2}x+3L{x}^2-x^3+3L^{2}x-6L{x}^2+3x^3-L{b}^2$

0=L3−3Lx2−Lb2$0=L^3-3L{x}^2-L{b}^2$

0=L2−3x2−b2$0=L^2-3x^2-b^2$

3x2=L2−b2$3x^2=L^2-b^2$

x=L2−b23−−−−−−−√$x=\sqrt{{\displaystyle \frac{L^2-b^2}{3}}}$   (okay!)