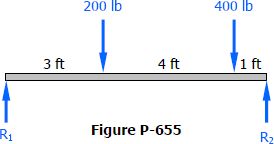
Find the value of EIδ under each concentrated load of the beam shown in Fig. P-655.

 Find the value of EIδ under each concentrated load of the beam shown in Fig..

 

ΣMR2=0ΣMR2=0

R1=200(5)+400(1)$8R_1=200(5)+400(1)$

R1=175 lb$R_1=175\text{ lb}$
 

ΣMR1=0$\mathrm{\Sigma }{M}_{R1}=0$

8R2=200(3)+400(7)$8R_2=200(3)+400(7)$

R2=425 lb$R_2=425\text{ lb}$
 

 

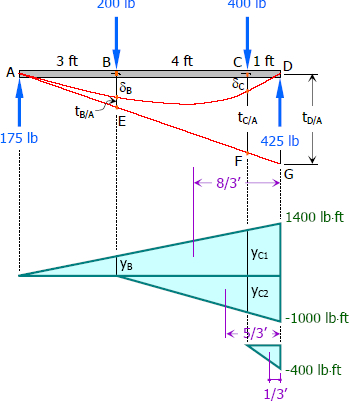
yC17=14008${\displaystyle \frac{y_{C1}}{7}}={\displaystyle \frac{1400}{8}}$

yC1=1225 lb$y_{C1}=1225\text{ lb}$
 

yC24=−10005${\displaystyle \frac{y_{C2}}{4}}={\displaystyle \frac{-1000}{5}}$

yC2=−800 lb$y_{C2}=-800\text{ lb}$
 

yB3=14008${\displaystyle \frac{y_B}{3}}={\displaystyle \frac{1400}{8}}$

yB=525 lb$y_B=525\text{ lb}$
 

EItD/A=(AreaAD)X¯D$EI{t}_{D/A}=(Are{a}_{AD}){\overline{X}}_D$

EItD/A=12(8)(1400)(83)−12(5)(1000)(53)−12(1)(400)(13)$EI{t}_{D/A}=\frac{1}{2}(8)(1400)(\frac{8}{3})-\frac{1}{2}(5)(1000)(\frac{5}{3})-\frac{1}{2}(1)(400)(\frac{1}{3})$

EItD/A=10700 lb⋅ft3$EI{t}_{D/A}=10700\text{ lb}\cdot {\text{ft}}^3$
 

EItC/A=(AreaAC)X¯C$EI{t}_{C/A}=(Are{a}_{AC}){\overline{X}}_C$

EItC/A=12(7)(yC1)(73)−12(4)(yC2)(43)$EI{t}_{C/A}=\frac{1}{2}(7)(y_{C1})(\frac{7}{3})-\frac{1}{2}(4)(y_{C2})(\frac{4}{3})$

EItC/A=12(7)(1225)(73)−12(4)(800)(43)$EI{t}_{C/A}=\frac{1}{2}(7)(1225)(\frac{7}{3})-\frac{1}{2}(4)(800)(\frac{4}{3})$

EItC/A=472256 lb⋅ft3$EI{t}_{C/A}=\frac{47225}{6}\text{ lb}\cdot {\text{ft}}^3$
 

EItB/A=(AreaAB)X¯B$EI{t}_{B/A}=(Are{a}_{AB}){\overline{X}}_B$

EItC/A=12(3)(yB)(1)$EI{t}_{C/A}=\frac{1}{2}(3)(y_B)(1)$

EItC/A=12(3)(525)(1)$EI{t}_{C/A}=\frac{1}{2}(3)(525)(1)$

EItC/A=15752 lb⋅ft3$EI{t}_{C/A}=\frac{1575}{2}\text{ lb}\cdot {\text{ft}}^3$
 

By ratio and proportion:
BE¯3=CF¯7=tD/A8${\displaystyle \frac{\overline{BE}}{3}}={\displaystyle \frac{\overline{CF}}{7}}={\displaystyle \frac{t_{D/A}}{8}}$

BE¯=38tD/A=38(10700)=80252$\overline{BE}=\frac{3}{8}{t}_{D/A}=\frac{3}{8}(10700)=\frac{8025}{2}$

CF¯=78tD/A=78(10700)=187252$\overline{CF}=\frac{7}{8}{t}_{D/A}=\frac{7}{8}(10700)=\frac{18725}{2}$
 

Deflections:
δB=BE¯−tB/A${\delta }_B=\overline{BE}-t_{B/A}$

EIδB=EIBE¯−EItB/A=80252−15752$EI{\delta }_B=EI\overline{BE}-EI{t}_{B/A}=\frac{8025}{2}-\frac{1575}{2}$

EIδB=3225 lb⋅ft3$EI{\delta }_B=3225\text{ lb}\cdot {\text{ft}}^3$            → answer
 

δC=CF¯−tC/A${\delta }_C=\overline{CF}-t_{C/A}$

EIδC=EICF¯−EItC/A=187252−472256$EI{\delta }_C=EI\overline{CF}-EI{t}_{C/A}=\frac{18725}{2}-\frac{47225}{6}$

EIδC=44753=1491.67 lb⋅ft3$$EIδC=44753=1491.67 lb⋅ft3           answer