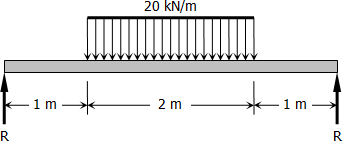
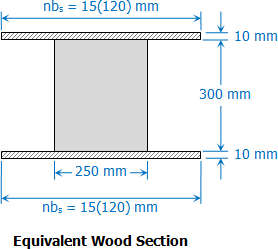
A simply supported beam 4 m long has the cross section shown in Fig. . It carries a uniformly distributed load of 20 kN/m over the middle half of the span. If n = 15, compute the maximum stresses in the wood and the steel.
Solution
R=12(20)(2)=20 kN
Maximum moment will occur at the midspan:
Mmax=2R−20(1)(0.5)=2(20)−10
Mmax=30 kN⋅m
Flexural stress:
fb=MyI
Where:
M=Mmax=30 kN⋅m
I=15(120)(300+10+10)312−[15(120)−250](3003)12
I=1427700000 mm4
Maximum stress in the wood (y = 150 mm)
fbw=30(150)(10002)1427700000
fbw=3.152 MPa
Maximum stress in the steel (y = 160 mm)
fbs15=30(160)(10002)1427700000
fbs=47.279 MPa
No comments:
Post a Comment