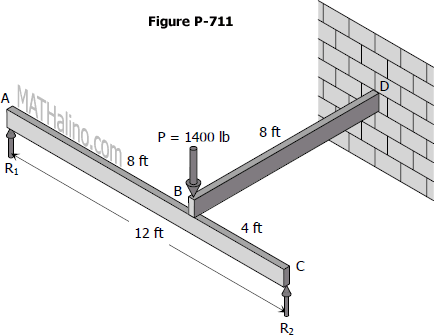
A cantilever beam BD rests on a simple beam AC as shown in Fig. P-711. Both beams are of the same material and are 3 in wide by 8 in deep. If they jointly carry a load P = 1400 lb, compute the maximum flexural stress developed in the beams.

A cantilever beam BD rests on a simple beam AC as shown in Fig. P-711. Both beams are of the same material and are 3 in wide by 8 in deep. If they jointly carry a load P = 1400 lb, compute the maximum flexural stress developed in the beams.
 

Solution

 For cantilever beam BD

From Case No. 1 of beam loading cases, the maximum deflection at the end of cantilever beam due to concentrated force at the free end is given by
 

δ=PL33EI$\delta ={\displaystyle \frac{P{L}^3}{3EI}}$

 

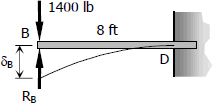Thus,
δB=1400(83)3EI−RB(83)3EI${\delta }_B={\displaystyle \frac{1400(8^3)}{3EI}}-{\displaystyle \frac{R_B(8^3)}{3EI}}$

δB=7168003EI−512RB3EI${\delta }_B={\displaystyle \frac{716800}{3EI}}-{\displaystyle \frac{512R_B}{3EI}}$
 

For the simple beam AC
The deflection at distance x from Case No. 7 of different beam loadings is
 

EIy=Pbx6L(L2–x2–b2)$EIy={\displaystyle \frac{Pbx}{6L}}(L^2–x^2–b^2)$   for   0<x<a$0<x<a$

 

For x=a$x=a$, the deflection equation will become
 

EIy=Pab6L(L2–a2–b2)$EIy={\displaystyle \frac{Pab}{6L}}(L^2–a^2–b^2)$

 

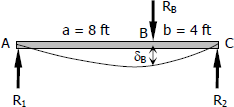For beam AC; P = RB, a = 8 ft, b = 4 ft, and L = 12 ft.

δB=RB(8)(4)6(12)EI(122–82–42)${\delta }_B={\displaystyle \frac{R_B(8)(4)}{6(12)EI}}({12}^2–8^2–4^2)$

δB=4RB9EI(64)${\delta }_B={\displaystyle \frac{4R_B}{9EI}}(64)$

δB=256RB9EI${\delta }_B={\displaystyle \frac{256R_B}{9EI}}$
 

Solving for the contact force, RB
δB=δB${\delta }_B={\delta }_B$

7168003EI−512RB3EI=256RB9EI${\displaystyle \frac{716800}{3EI}}-{\displaystyle \frac{512R_B}{3EI}}={\displaystyle \frac{256R_B}{9EI}}$

7168003EI=1972RB9EI${\displaystyle \frac{716800}{3EI}}={\displaystyle \frac{1972R_B}{9EI}}$

RB=1200 lb$R_B=1200\text{ lb}$
 

Determining the maximum moment
The maximum moment on cantilever beam will occur at D
MD=1200(8)–1400(8)$M_D=1200(8)–1400(8)$

MD=–1600 lb⋅ft$M_D=–1600\text{ lb}\cdot \text{ft}$
 

The maximum moment on simple beam will occur at point B.
MB=PabL=1200(8)(4)12$M_B={\displaystyle \frac{Pab}{L}}={\displaystyle \frac{1200(8)(4)}{12}}$

MB=3200 lb⋅ft$M_B=3200\text{ lb}\cdot \text{ft}$
 

Maximum moment is at point B
Mmax=3200 lb⋅ft$M_{max}=3200\text{ lb}\cdot \text{ft}$
 

Solving for maximum flexural stress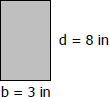
The bending stress of rectangular beam is given by
fb=6Mbd2$f_b={\displaystyle \frac{6M}{b{d}^2}}$

Thus,
(fb)max=6(3200)(12)3(82)$(f_b{)}_{max}={\displaystyle \frac{6(3200)(12)}{3(8^2)}}$

(fb)max=1200 psi$(f_b{)}_{max}=1200\text{ psi}$           answer