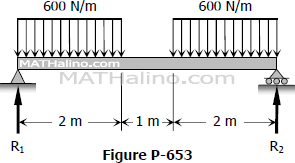
Compute the midspan value of EIδ for the beam shown in Fig. . (Hint: Draw the M diagram by parts, starting from midspan toward the ends. Also take advantage of symmetry.

Compute the midspan value of EIδ for the beam shown in Fig. . (Hint: Draw the M diagram by parts, starting from midspan toward the ends. Also take advantage of symmetry.
 

Solution (Using Moment Diagram by Parts)

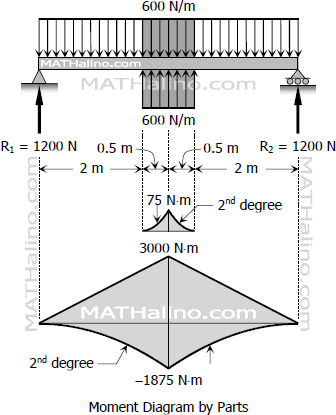
 By symmetry,

R1=R2=2(600)$R_1=R_2=2(600)$

R1=R2=1200 N$R_1=R_2=1200\text{ N}$
 

 

 

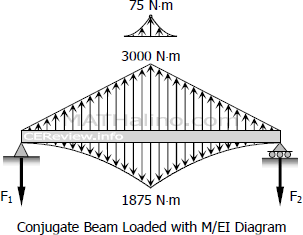
The loads of conjugate beam are symmetrical, thus,
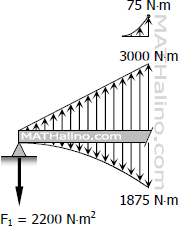
F1=F2=12[12(5)(3000)+13(1)(75)−13(5)(1875)]$F_1=F_2=\frac{1}{2}[\frac{1}{2}(5)(3000)+\frac{1}{3}(1)(75)-\frac{1}{3}(5)(1875)]$

F1=F2=2200 N⋅m2$F_1=F_2=2200\text{ N}\cdot {\text{m}}^2$
 

For this beam, the maximum deflection will occur at the midspan.
 

 

Mmidspan=12(2.5)(3000)[13(2.5)]+13(0.5)(75)[14(0.5)]−13(2.5)(1875)[14(2.5)]−2200(2.5)$M_{midspan}=\frac{1}{2}(2.5)(3000)[\frac{1}{3}(2.5)]+\frac{1}{3}(0.5)(75)[\frac{1}{4}(0.5)]-\frac{1}{3}(2.5)(1875)[\frac{1}{4}(2.5)]-2200(2.5)$

Mmidspan=−3350 N⋅m3$M_{midspan}=-3350\text{ N}\cdot {\text{m}}^3$
 

Therefore, the maximum deflection is
EI δmax=Mmidspan$EI{\delta }_{max}=M_{midspan}$

EI δmax=−3350 N⋅m3$EI{\delta }_{max}=-3350\text{ N}\cdot {\text{m}}^3$

EI δmax=3350 N⋅m3$EI{\delta }_{max}=3350\text{ N}\cdot {\text{m}}^3$   below the neutral axis           answer