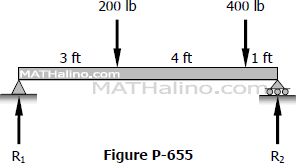
Find the value of EIδ under each concentrated load of the beam shown in Fig

 Find the value of EIδ under each concentrated load of the beam shown in Fig. 

 

Solution 

ΣMD=0ΣMD=0

8R1=200(5)+400(1)$8R_1=200(5)+400(1)$

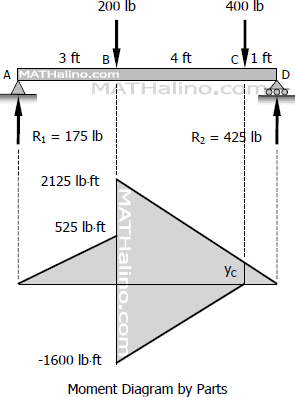
R1=175 lb$R_1=175\text{ lb}$
 

ΣMA=0$\mathrm{\Sigma }{M}_A=0$

8R2=200(3)+400(7)$8R_2=200(3)+400(7)$

R2=425 lb$R_2=425\text{ lb}$
 

 

By ratio and proportion
yC1=21255${\displaystyle \frac{y_C}{1}}={\displaystyle \frac{2125}{5}}$

yC=425 lb⋅ft$y_C=425\text{ lb}\cdot \text{ft}$
 

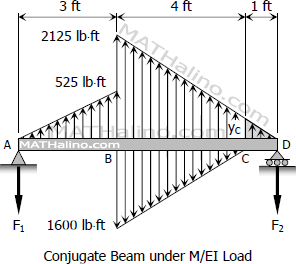
From the conjugate beam
ΣMD=0$\mathrm{\Sigma }{M}_D=0$

8F1+12(4)(1600)[1+23(4)]=12(3)(525)[5+13(3)]+12(5)(2125)[23(5)]$8F_1+\frac{1}{2}(4)(1600)[1+\frac{2}{3}(4)]=\frac{1}{2}(3)(525)[5+\frac{1}{3}(3)]+\frac{1}{2}(5)(2125)[\frac{2}{3}(5)]$

F1=1337.5 lb⋅ft2$F_1=1337.5\text{ lb}\cdot {\text{ft}}^2$
 

 

ΣMA=0$\mathrm{\Sigma }{M}_A=0$

8F2+12(4)(1600)[13(4)]=12(3)(525)[23(3)]+12(5)(2125)[3+13(5)]$8F_2+\frac{1}{2}(4)(1600)[\frac{1}{3}(4)]=\frac{1}{2}(3)(525)[\frac{2}{3}(3)]+\frac{1}{2}(5)(2125)[3+\frac{1}{3}(5)]$

F2=1562.5 lb⋅ft2$F_2=1562.5\text{ lb}\cdot {\text{ft}}^2$
 

Consider the section to the left of B in conjugate beam
MB=12(3)(525)[13(3)]−3F1$M_B=\frac{1}{2}(3)(525)[\frac{1}{3}(3)]-3F_1$

MB=787.5−3(1337.5)$MB=787.5-3(1337.5)$

MB=−3225 lb⋅ft3$M_B=-3225\text{ lb}\cdot {\text{ft}}^3$
 

Thus, the deflection at B is
EI δB=MB$EI{\delta }_B=M_B$

EI δB=3225 lb⋅ft3$EI{\delta }_B=3225\text{ lb}\cdot {\text{ft}}^3$           answer
 

Consider the section to the right of C in conjugate beam
MC=12(1)(yC)[13(1)]−1F2$M_C=\frac{1}{2}(1)(y_C)[\frac{1}{3}(1)]-1F_2$

MC=12(1)(425)[13(1)]−1(1562.5)$M_C=\frac{1}{2}(1)(425)[\frac{1}{3}(1)]-1(1562.5)$

MC=−1491.67 lb⋅ft3$M_C=-1491.67\text{ lb}\cdot {\text{ft}}^3$
 

Thus, the deflection at C is
EI δC=MC$EI{\delta }_C=M_C$

EI δC=−1491.67 lb⋅ft3$EI{\delta }_C=-1491.67\text{ lb}\cdot {\text{ft}}^3$

EI δC=1491.67 lb⋅ft3$EI{\delta }_C=1491.67\text{ lb}\cdot {\text{ft}}^3$   downward           answer