Two timber beams are mounted at right angles and in contact with each other at their midpoints. The upper beam A is 2 in wide by 4 in deep and simply supported on an 8-ft span; the lower beam B is 3 in wide by 8 in deep and simply supported on a 10-ft span. At their cross-over point, they jointly support a load P = 2000 lb. Determine the contact force between the beams.

Two timber beams are mounted at right angles and in contact with each other at their midpoints. The upper beam A is 2 in wide by 4 in deep and simply supported on an 8-ft span; the lower beam B is 3 in wide by 8 in deep and simply supported on a 10-ft span. At their cross-over point, they jointly support a load P = 2000 lb. Determine the contact force between the beams.
 

Solution

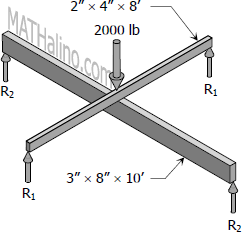Let
R = contact force between beams A and B
Subscript ( A ) = for upper beam
Subscript ( B ) = for lower beam
 

Moment of inertia
IA=2(43)12=323 in4$I_A={\displaystyle \frac{2(4^3)}{12}}={\displaystyle \frac{32}{3}}{\text{ in}}^4$

IB=3(83)12=128 in4$I_B={\displaystyle \frac{3(8^3)}{12}}=128{\text{ in}}^4$
 

Note:
The midspan deflection of a simple beam loaded with concentrated force at the midpoint is given by
 

δ=PL348EI$\delta ={\displaystyle \frac{P{L}^3}{48EI}}$

 

See Case No. 6 in the Summary of Beam Loadings.
 

The midspan of upper beam A is under 2000 lb applied load and contact force R. R will act upward at beam A.
δA=2000(83)(123)48E(323)−R(83)(123)48E(323)${\delta }_A={\displaystyle \frac{2000(8^3)({12}^3)}{48E(\frac{32}{3})}}-{\displaystyle \frac{R(8^3)({12}^3)}{48E(\frac{32}{3})}}$

δA=3456000E−1728RE${\delta }_A={\displaystyle \frac{3456000}{E}}-{\displaystyle \frac{1728R}{E}}$
 

The lower beam B is subjected by the contact force R at midspan.
δB=R(103)(123)48E(128)${\delta }_B={\displaystyle \frac{R({10}^3)({12}^3)}{48E(128)}}$

δB=1125R4E${\delta }_B={\displaystyle \frac{1125R}{4E}}$
 

The deflections of upper beam A and lower beam B are obviously equal. R will act downward at beam B.
δA=δB${\delta }_A={\delta }_B$

3456000E−1728RE=1125R4E${\displaystyle \frac{3456000}{E}}-{\displaystyle \frac{1728R}{E}}={\displaystyle \frac{1125R}{4E}}$

3456000=8037R4$3456000={\displaystyle \frac{8037R}{4}}$

R=1720.04 lb$R=1720.04\text{ lb}$           answer