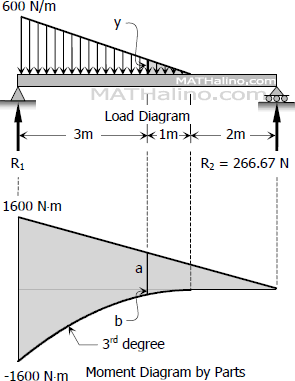
 From the load diagram
From the load diagram
ΣMR1=06R2=12(4)(600)[13(4)]
R2=266.67 N
y1=6004
y=150 N/m
From the moment diagram
a=3R2=3(266.67)
a=800 N⋅m
b=−12(1)(y)[13(1)]
b=−16y=−16(150)
b=−25 N⋅m
From the conjugate beam
ΣMF1=0
6F2+14(4)(1600)[15(4)]=12(6)(1600)[13(6)]
F2=1386.67 N⋅m2
Mmidspan=12(3a)[13(3)]−14(1b)[15(1)]−3F2
Mmidspan=12(3)(800)[13(3)]−14(1)(25)[15(1)]−3(1386.67)
Mmidspan=−2961.25 N⋅m3
Thus, the deflection at the midspan is
EIδm=Mmidspan
EIδm=−2961.25 N⋅m3
EIδm=2961.25 N⋅m3 below the neutral axis answer
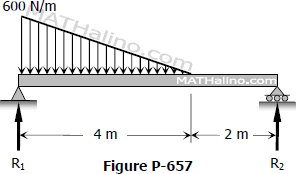
 From the load diagram
From the load diagram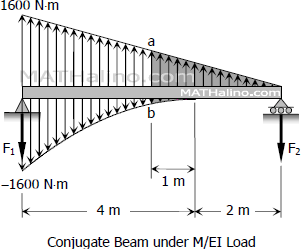

 From the load diagram
From the load diagram
No comments:
Post a Comment